Some geometry you don't need to know, but might be interesting to you...
I wondered if the beach propeller shape had a name, and what was its nature? I knew about the hexafoil or "flower of life," which has 6 blades with sharp tips. I learned about some related shapes: trefoil, trefoil knot, triquetra, and trillium flowers. Finally, I delved into some mathematical approaches, and found this (click to play the video):
This is a parametric curve, defined by two equations. As time (t) progresses, the x and y coordinates are given by: x=sin(t)+sin(2t) and y=cos(t)-cos(2t). I don't know if this is the exact shape of the sand propeller my body/mind instinctively makes. It would be nice to have an aerial photo of a sand propeller and check to see if this is true. This shape has some surprising properties. One interesting thing you can see in the animation above is that the mover slows down for the sharper curves and speeds up for the straighter sections. This is the same as what our bodies do. If the math of this interests you, you can download the excel simulation I made.
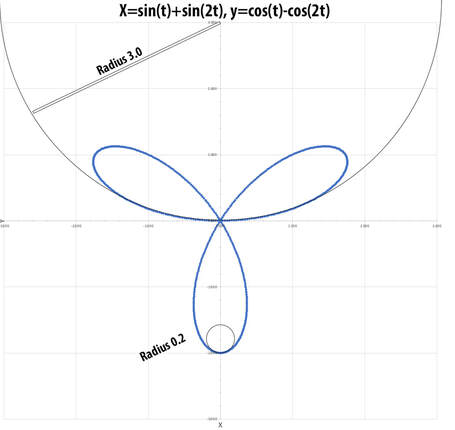
The simulation I made includes some calculations about the "radius of curvature." You can see that the path is most curved at the tips, and least curved at the center. Radius of curvature is a way to describe this. Surprisingly, the radius of curvature at the tips is exactly 1/10 of the length of the propeller "blade," and at the center the radius of curvature is exactly 1.5 times the blade length.
Maybe you are wondering about banked curves? You don't have to run to enjoy a beach propeller. But if you do run, your body knows exactly how much to lean in on the curves. Even though you go slower at the tips of the propeller, that is still where the degree of banking (leaning) is the most. I hope someone will do the physics, make a graph of the banking angle, and send that to me.
Maybe you are wondering about banked curves? You don't have to run to enjoy a beach propeller. But if you do run, your body knows exactly how much to lean in on the curves. Even though you go slower at the tips of the propeller, that is still where the degree of banking (leaning) is the most. I hope someone will do the physics, make a graph of the banking angle, and send that to me.